warunki brzegowe
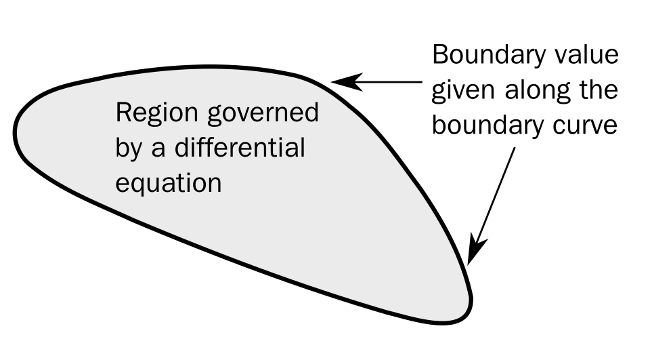
Warunki brzegowe — Warunki brzegowe – zespół warunków, które muszą być spełnione dla uzyskania rozwiązania równania różniczkowego (zwyczajnego lub cząstkowego) w punktach położonych na brzegu obszaru zdefiniowanego dla danej funkcji, by rozwiązanie było jednoznaczne we wszystkich punktach danego obszaru; wyróżnia się warunki brzegowe Dirichleta (I rodzaju), Neumanna (II rodzaju), Robina (III rodzaju), mieszane warunki brzegowe oraz warunki brzegowe Cauchy’ego (warunki początkowe).
Warunek brzegowy Dirichleta (warunek brzegowy I rodzaju) zakłada, że funkcja stanowiąca rozwiązanie danego równania różniczkowego (zwyczajnego lub cząstkowego) musi przyjmować określone, zadane wartości na brzegu dziedziny (zdefiniowanego dla tej funkcji obszaru). Nazwa pochodzi od nazwiska niemieckiego matematyka Petera Gustava Lejeune Dirichleta.
Dla równania różniczkowego zwyczajnego II-rzędu:gdzie:
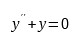
niewiadoma funkcja y (x) określona jest na dziedzinie [a,b] , warunki brzegowe Dirichleta przyjmują następującą postać:
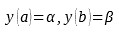
gdzie: α i β i są danymi liczbami.
Dla równania różniczkowego cząstkowego:
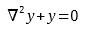
gdzie: ∇2 – operator Laplace’a (operator różniczkowy drugiego rzędu), warunki brzegowe Dirichleta w domenie Ω ⊂ Rn przyjmują postać:
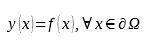
gdzie: f jest funkcją zdefiniowaną na granicy ∂ Ω.
Warunki brzegowe Dirichleta pełnią ważną rolę w opisie wielu zjawisk fizycznych:
- w termodynamice w opisie zjawiska transportu energii wewnętrznej (rozchodzenia się ciepłatemperaturą na całej powierzchni;
- w elektrostatyce przy określaniu funkcji potencjału elektrycznego; przyjęcie warunku brzegowego oznacza, że węzeł obwodu jest utrzymywany w stałym napięciu;
- w teorii sprężystości przyjęcie warunku brzegowego oznacza, że koniec pręta utrzymywany jest w stałej pozycji w stosunku do punktów brzegowych;
- w mechanice płynów przyjmuje się, że na brzegu cząsteczki płynów się nie poruszają (no-slip); podczas przepływu lepkiej cieczy po powierzchni ciała stałego, płyn ten ma zerową prędkość względem brzegu.
- w modelach filtracji wód podziemnych warunek brzegowy określa wartość wysokości hydraulicznej w określonych punktach (np. wzdłuż brzegu modelowanego obszaru filtracji).

Warunek brzegowy Neumanna
Warunek brzegowy Neumanna (warunek brzegowy II rodzaju) zakłada, że pochodna funkcji stanowiącej rozwiązanie danego równania różniczkowego (zwyczajnego lub cząstkowego) przyjmuje określoną wartość wzdłuż normalnej zewnętrznej do brzegu obszaru. Nazwa pochodzi od nazwiska niemieckiego matematyka Carla Gottfrieda Neumanna.
Dla równania różniczkowego zwyczajnego:
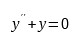
warunki graniczne Neumanna w dziedzinie [a, b] przyjmują postać:
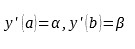
gdzie: α i β i są danymi liczbami.
Dla równania różniczkowego cząstkowego:
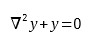
gdzie: ∇2 – operator Laplace’a, warunki brzegowe Neumanna w domenie Ω ⊂ Rn przyjmują postać:
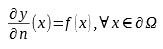
gdzie:
- n – normalna zewnętrzna (wektor normalny zewnętrzny) dla granicy ∂ Ω
- f – funkcja zdefiniowana na granicy ∂ Ω
Pochodna wektora normalnego jest zdefiniowana jako:
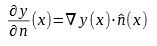
gdzie:
- ∇ y (x) oznacza gradient y(x)
- n^– jednostkę wektora normalnego
- oznacza operator przestrzeni unitarnej – przestrzeni liniowej (wektorowej)
Warunek brzegowy Neumanna opisuje następujące zjawiska fizyczne:
- w termodynamice określa wartość strumienia ciepła; np. izolator termiczny cechuje się małą przewodnością cieplną; przewodnik (np. koniec żelaznego pręta przy którym znajduje się grzejnik) rozprowadza ciepło ze stałą prędkością, ale rzeczywista temperatura nie jest znana.
- w modelach filtracji wód podziemnych określa wartość strumienia filtracji w kierunku prostopadłym do brzegu obszaru; w przypadku brzegu nieprzepuszczalnego wartość ta jest równa zeru.
Warunek brzegowy Robina
Warunek brzegowy Robina (warunek brzegowy III rodzaju) stanowi kombinację liniowej wartości funkcji oraz jej pochodnej normalnej na granicy obszaru zdefiniowanego dla tej funkcji (średnią ważoną funkcji i pochodnej). Nazwa pochodzi od nazwiska francuskiego matematyka Victora Gustave’a Robina.
Warunek brzegowy Robina w domenie Ω i granicy ∂ Ω dla niezerowych stałych (funkcji) a i b oraz zadanej funkcji g zdefiniowanej na granicy ∂ Ω , przyjmuje następującą postać:
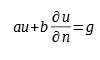
gdzie:
- u – nieznane rozwiązanie zdefiniowane w Ω
- ∂u/∂n – normalna pochodna na granicy ∂ Ω
Warunki brzegowe Robina wykorzystywane są w zagadnieniach dotyczących elektromagnetyzmu (warunki brzegowe impedancji) oraz procesów wymiany ciepła (konwekcyjne warunki brzegowe).

Mieszany warunek brzegowy
Mieszany warunek brzegowy stanowi połączenie warunków brzegowych Dirichleta i Neumanna. Rozwiązanie danego równania różniczkowego polega na znalezieniu w obszarze Ω funkcji o zadanej kombinacji liniowej wraz z pochodną normalną zdefiniowaną na brzegu ∂ Ω .
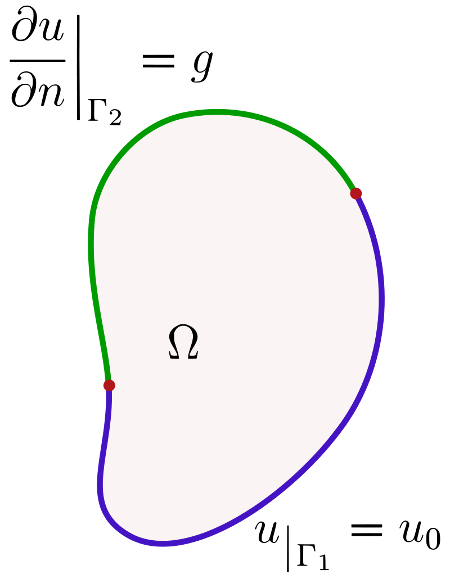
Rozwiązanie równania różniczkowego cząstkowego u w domenie Ω z granicą ∂ Ω spełnia mieszany warunek brzegowy, jeśli zawierając granice ∂ Ω dwóch rozłącznych części obszaru Г1 i Г2 (przy założeniu, że ∂Ω = Г1UГ2 ) u wyraża się następującymi równaniami:
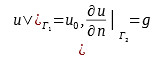
gdzie: u0 i g są funkcjami zdefiniowanymi na tych częściach granicy.
Warunek brzegowy Cauchy’ego (warunek początkowy)
Warunek brzegowy Cauchy’ego (warunek początkowy) dla funkcji spełniającej dane równanie różniczkowe II-rzędu (zwyczajne lub cząstkowe) określa punkt, przez który będzie przechodzić wykres tej funkcji oraz wartość pochodnej tej funkcji na granicy zdefiniowanego dla niej obszaru – czyli obejmuje warunki brzegowe Dirichleta i Neumanna. Nazwa pochodzi od francuskiego analityka matematycznego Augustina Louisa Cauchy’ego. Zagadnienie to wykorzystywane jest np. w opisie ruchu falowego (równanie falowe).