energia kinetyczna
Energia kinetyczna — Energia kinetyczna – część energii mechanicznej układu fizycznego. Energia kinetyczna to energia, którą posiada ciało znajdujące się w ruchu względem określonego układu odniesienia. Wartość energii kinetycznej ciała o masie m jest wprost proporcjonalna do kwadratu prędkości, z którą porusza się ciało, lecz nie zależy od kierunku i zwrotu wektora prędkości.
Energia
Energia jest skalarną wielkością fizyczną umożliwiającą opis procesów oraz oddziaływań zachodzących w danym układzie fizycznym; jest miarą zdolności danego układu do wykonywania pracy. Energia w przyrodzie występuje w różnych formach – jako energia cieplna, energia elektryczna, energia mechaniczna, energia chemiczna czy energia fal elektromagnetycznych. W układzie zamkniętym zgodnie z zasadą zachowania energii suma wszystkich rodzajów energii jest stała w czasie – energia nie może zostać utworzona na nowo ani zostać zniszczona, możliwa jest tylko przemiana jednych form energii w inne.
Energia mechaniczna jest energią związaną z ruchem mechanicznym i położeniem układu fizycznego względem określonego układu odniesienia bądź ruchem i położeniem elementów składowych tego układu względem siebie. Energia mechaniczna stanowi sumę energii kinetycznej (energii, jaką posiada ciało będące w ruchu) oraz energii potencjalnej (energii, jaką posiada dane ciało w zależności od położenia w przestrzeni).
Energia kinetyczna ciała poruszającego się ruchem postępowym
Energia kinetyczna jest energią, którą posiada ciało znajdujące się w ruchu względem określonego układu odniesienia, jak np. biegnący człowiek, jadący samochód, lecący samolot, rzucona piłka, strzała wystrzelona z łuku, tocząca się kula. Energia kinetyczna danego ciała nie jest niezmienna, gdyż zależy od przyjętego układu odniesienia. Może być przekazywana pomiędzy ciałami, np. podczas zderzenia kul jedna z nich przekazuje drugiej energię kinetyczną, co powoduje poruszanie się drugiej kuli z większą prędkością, podczas gdy pierwsza kula zwalnia, a następnie zatrzymuje się.
Aby dane ciało uzyskało energię kinetyczną nad tym ciałem musi zostać wykonana określona praca, która umożliwia rozpędzenie ciała do prędkości, z jaką się porusza (np. rzucenie piłki, naciągnięcie i puszczenie cięciwy łuku). Zmiana energii danego ciała jest równa pracy siły zewnętrznej wykonanej nad tym ciałem:
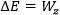
Zmiana energii kinetycznej danego ciała jest możliwa wyłącznie w wypadku, gdy działające na to ciało siły nie równoważą się, a wypadkowa tych sił (zgodnie z II zasadą dynamiki Newtona) nadaje temu ciału przyspieszenie, więc ulega zmianie prędkość, z którą porusza się to ciało.
Energia kinetyczna (Ek) ciała o masie m poruszającego się ruchem postępowym jest wprost proporcjonalna do masy ciała i kwadratu prędkości v, z jaką porusza się ciało (dużo mniejszą od prędkości światła w próżni c), lecz nie zależy od kierunku i zwrotu wektora prędkości. Zależność tą można przedstawić równaniem:
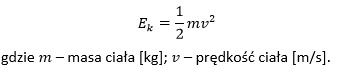
Jednostką energii kinetycznej jest dżul (J), który równy jest energii (pracy) wykonanej przez siłę o wartości 1 niutona (N) podczas przesunięcia punktu przyłożenia siły o 1 metr (m) w kierunku równoległym do kierunku działania tej siły:
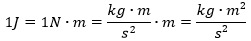
Nazwa dżul pochodzi od nazwiska angielskiego fizyka Jamesa Joule’a.
Związek energii kinetycznej z pędem ciała (p=mv) przedstawia się następującym równaniem:
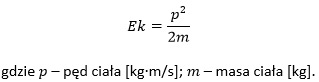

Energia kinetyczna ciała (bryły sztywnej) poruszającego się ruchem obrotowym
Ruch obrotowy bryły sztywnej jest ruchem, podczas którego wszystkie punkty bryły poruszają się po okręgach leżących na jednej prostej określanej jako oś obrotu. Energia kinetyczna bryły sztywnej poruszającej się ruchem obrotowym dla małych prędkości wynosi:

Zależność prędkości liniowej v ciała poruszającego się po okręgu o promieniu r od prędkości kątowej ω wyraża się wzorem:
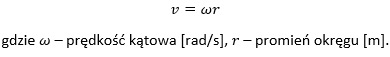
Moment bezwładności danego punktu materialnego bryły sztywnej jest iloczynem jego masy i kwadratu odległości od osi obrotu:
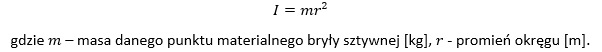
Energia kinetyczna bryły sztywnej obracającej się z prędkością kątową ω wokół jednej z osi głównych, z uwzględnieniem powyższych zależności, wyraża się następującym równaniem:
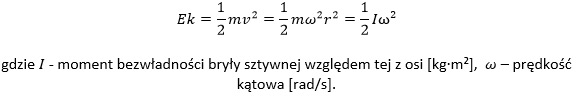
Energia kinetyczna w mechanice relatywistycznej
Dla ciał poruszających się z prędkościami zbliżonymi do prędkości światła (prędkościami relatywistycznymi) do obliczania energii kinetycznej wykorzystuje się wzór, w którym energia kinetyczna stanowi różnicę pomiędzy energią całkowitą a energią spoczynkową. Zależność tą można przedstawić wzorem:
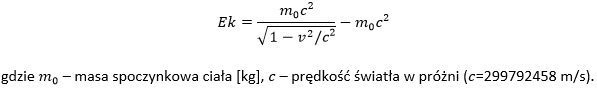
Energia kinetyczna w dynamice płynów
W dynamice płynów, działu mechaniki płynów zajmującego się ruchem płynów (cieczy lub gazów), stosunek energii kinetycznej na jednostkę objętości w każdym punkcie pola przepływu płynu nieściśliwego określany jest jako ciśnienie dynamiczne q w tym punkcie. Zależność ta wyraża się wzorem:
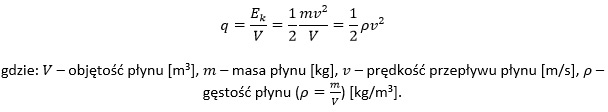







bardzo dobra odpowiedź
Plus za dodanie, ze ruch odbywa sie wzgledem ukladu odniesienia. Warto by jeszcze dodac, ze energia kinetyczna rowna jest pracy wykonanej do rozpedzenia ciala (tu wyprowadzenie wzoru: https://leszekbober.pl/energia-kinetyczna/) oraz ze energia kinetyczna moze zamienic sie na potencjalna (i odwrotnie)