horyzont
Horyzont – koło wielkie na sferze niebieskiej, leżące w płaszczyźnie poziomej prostopadłej do linii lokalnego pionu przechodzącej przez miejsce obserwacji i środek Ziemi oraz płaszczyźnie przechodzącej przez środek Ziemi oraz położonej równolegle do płaszczyzny horyzontu obserwatora oddalonej od powierzchni Ziemi o wysokość oczną, czyli wysokość wzniesienia oczu obserwatora (horyzont astronomiczny, horyzont rzeczywisty); bądź linia pozornego zetknięcia nieboskłonu z powierzchnią Ziemi, oddzielająca widoczną część sfery niebieskiej od jej niewidocznej części (horyzont widzialny, horyzont pozorny, widnokrąg).
Horyzont astronomiczny, horyzont widzialny i horyzont geometryczny
Horyzont astronomiczny, określany również mianem horyzontu rzeczywistego, definiowany jest jako koło wielkie na sferze niebieskiej położone w równej odległości od zenitu i nadiru obserwatora, czyli punktów przecięcia lokalnej osi pionu ze sferą niebieską. Płaszczyzna pozioma horyzontu astronomicznego jest prostopadła do osi lokalnego pionu przechodzącej przez miejsce obserwacji i środek Ziemi oraz w płaszczyźnie przechodzącej przez środek Ziemi leżącej równolegle do płaszczyzny horyzontu obserwatora, oddalonej od powierzchni Ziemi o tzw. wysokość oczną, czyli wysokość wzniesienia oczu obserwatora. Horyzont obserwatora ze względu na nieskończenie wielki promień sfery niebieskiej w stosunku do promienia Ziemi jest z założenia równy horyzontowi astronomicznemu.
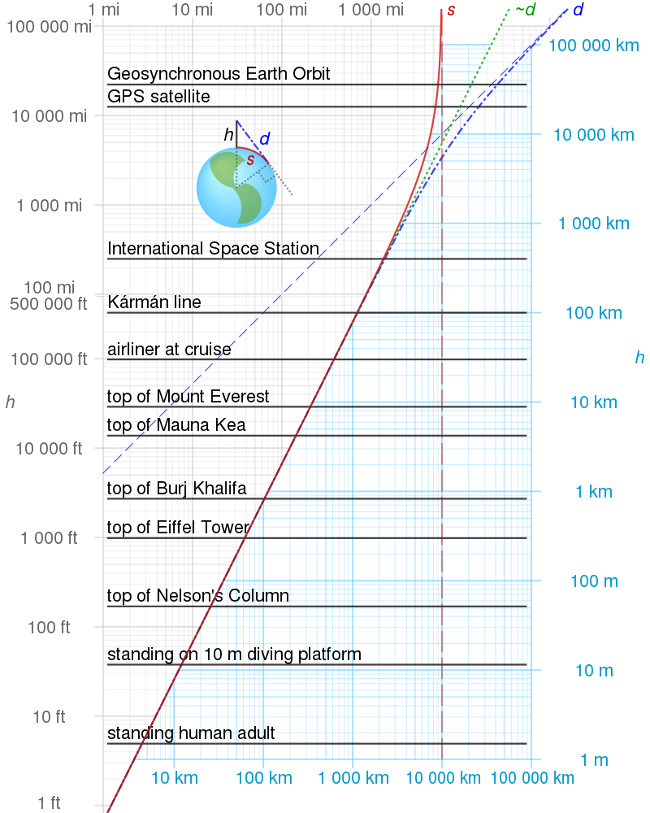
Horyzont widzialny, zwany także horyzontem pozornym bądź widnokręgiem, stanowi linia pozornego zetknięcia nieboskłonu z powierzchnią Ziemi, oddzielająca część sfery niebieskiej widoczną dla obserwatora od jej części niewidocznej. Średnica widnokręgu wzrasta wraz ze wzrostem wysokości położenia obserwatora, czyli im wyżej znajduje się miejsce obserwacji tym bardziej odległy jest widnokrąg oraz zwiększa się zasięg wzroku obserwatora. Odległość widnokręgu od obserwatora zwiększa się także pod wpływem zjawiska ugięcia promieni świetlnych w atmosferze ziemskiej, czyli refrakcji atmosferycznej. Kształt widnokręgu warunkuje stopień nierówności terenu; na otwartych, równinnych przestrzeniach bądź na pełnym morzu widnokrąg zbliżony jest kształtem do okręgu; na terenach pagórkowatych, wyżynnych, górzystych, zalesionych bądź zabudowanych jego kształt wyznaczają najdalsze, widoczne dla obserwatora elementy krajobrazu.
Horyzont geometryczny, zwany również horyzontem prawdziwym, stanowi płaszczyznę stożka o wierzchołku znajdującym się na wysokości oka obserwatora i stycznego do powierzchni Ziemi; linia styczna z powierzchnią Ziemi stanowi linię widnokręgu. Horyzont geometryczny położony jest poniżej horyzontu pozornego, w związku z czym odległość obserwatora do widnokręgu jest nieco mniejsza niż w przypadku horyzontu pozornego, gdzie za większą odległość od obserwatora odpowiedzialne jest zjawisko refrakcji atmosferycznej. Horyzont geometryczny obniżony jest względem horyzontu astronomicznego o kąt (γ) zawarty między horyzontem obserwatora a linią biegnącą od oczu obserwatora i styczną do powierzchni Ziemi, który wynosi:
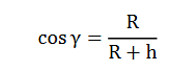
gdzie:
R – promień Ziemi,
h – wysokość obserwatora.
Wielkość obniżenia horyzontu prawdziwego w stosunku do horyzontu astronomicznego dla zwykłych obserwacji prowadzonych z powierzchni Ziemi (gdzie h jest wysokością wzniesienia oczu obserwatora ponad powierzchnię Ziemi) jest niewielka; jednak wraz z rosnącym wzrostem wysokości położenia obserwatora staje się coraz bardziej znacząca.

Odległość horyzontu geometrycznego od obserwatora
Odległość horyzontu geometrycznego (prawdziwego) do obserwatora z pominięciem efektu zjawiska refrakcji atmosferycznej można obliczyć z wykorzystaniem wzoru wyprowadzonego w oparciu o twierdzenie Pitagorasa. Widnokrąg (d), linia styczna do powierzchni Ziemi (s), oddzielająca część sfery niebieskiej znajdującą się w zasięgu wzroku obserwatora od jej części niewidocznej, jest linią prostopadłą do promienia Ziemi (R). Linia widnokręgu (d), wyznaczająca odległość obserwatora do horyzontu prawdziwego (H), wraz z promieniem Ziemi (R) stanowią dwie przyprostokątne trójkąta prostokątnego; przeciwprostokątna stanowi sumę promienia Ziemi i wysokości ocznej obserwatora (R + h).
Zgodnie z treścią twierdzenia Pitagorasa suma kwadratów długości przyprostokątnych (suma kwadratów odległości obserwatora do horyzontu geometrycznego oraz promienia Ziemi) jest równa kwadratowi długości przeciwprostokątnej (kwadratowi sumy promienia Ziemi oraz wysokości ocznej obserwatora):
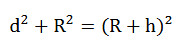
gdzie:
d – odległość do horyzontu geometrycznego [km],
R – promień Ziemi [km] ( = 6371 km),
h – wysokość oczna obserwatora nad powierzchnią Ziemi [m].
Wzór na odległość obserwatora do horyzontu geometrycznego (d) wyprowadzany jest na drodze przekształceń powyższego zapisu twierdzenia Pitagorasa zgodnie z równaniami:
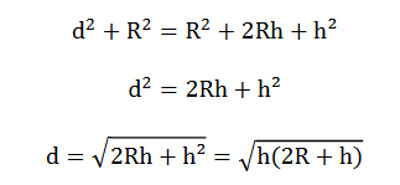
gdzie:
d – odległość do horyzontu geometrycznego [km],
r – promień Ziemi [km] ( = 6371 km),
h – wysokość oczna obserwatora nad powierzchnią Ziemi [m].
Jeżeli obserwacja prowadzona jest blisko powierzchni Ziemi, można pominąć wysokość oczną obserwatora (h) w wyrażeniu (2R + h) wówczas odległość obserwatora od horyzontu geometrycznego (d) można przedstawić w postaci poniższego wzoru:
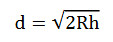
Podstawiając do powyższego równania długość średniego promienia Ziemi wynoszącą 6371 km, otrzymujemy wzór na przybliżoną odległość obserwatora do horyzontu geometrycznego:
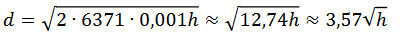
Powyższy wzór ma zastosowanie w przypadku, gdy wysokość oczna obserwatora (h) jest znacznie mniejsza od długości promienia Ziemi (np. obserwacji prowadzonej w pobliżu powierzchni Ziemi, z dachu 100-metrowego wieżowca bądź ze szczytu górskiego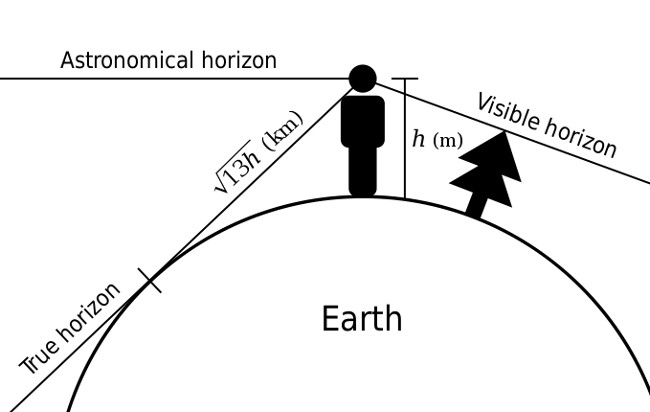
Wpływ refrakcji atmosferycznej na odległość do widnokręgu
Refrakcja atmosferyczna jest zjawiskiem polegającym na ugięciu, czyli zmianie kierunku rozchodzenia się promieni świetlnych przechodzących przez atmosferę ziemską. Stopień załamania promieni świetlnych w tym niejednorodnym ośrodku zależy głównie od gęstości powietrza, warunkowanej przez ciśnienie atmosferyczne oraz temperaturę powietrza, które z kolei zależne są od wysokości nad poziomem morza. Współczynnik załamania światła jest większy w pobliżu powierzchni Ziemi niż w wyższych partiach atmosfery ze względu na większą gęstość powietrza na niewielkich wysokościach. Zjawisko refrakcji atmosferycznej powoduje, że rzeczywista odległość obserwatora do widnokręgu jest nieco większa niż odległość obliczona za pomocą wzorów geometrycznych.
Rzeczywistą odległość obserwatora do widnokręgu (d) można obliczyć przyjmując założenie, że krzywizna toru promienia świetlnego ugiętego wskutek refrakcji jest stała i promień ten biegnie po łuku okręgu. Wielkość tę można opisać za pomocą współczynnika refrakcji wyrażającego stosunek między promieniem krzywizny Ziemi a promieniem krzywizny toru promienia świetlnego (R’) zgodnie z zależnością:
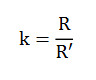
gdzie:
k – współczynnik refrakcji,
R – promień krzywizny kuli ziemskiej [km] ( = 6371 km),
R’ – promień krzywizny toru promienia świetlnego [km].
Współczynnik refrakcji w standardowych warunkach atmosferycznych dla promienia krzywizny kuli ziemskiej o długości 6371 km oraz promienia krzywizny toru promienia świetlnego długości o 43880 km przyjmuje wartość 1/6,918, co oznacza iż promień krzywizny toru promienia świetlnego (R’) jest około 7-krotnie większy w porównaniu do promienia krzywizny kuli ziemskiej (R).
Rzeczywista odległość obserwatora do widnokręgu (d) przy założeniu, że wysokość oczna obserwatora jest znacznie mniejsza od długości promienia krzywizny kuli ziemskiej (h << R), może być obliczona na podstawie poniższej zależności:
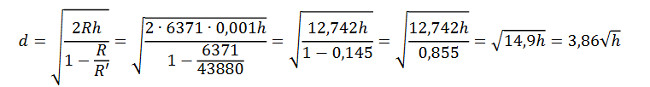
gdzie:
d – rzeczywista odległość obserwatora do widnokręgu [km],
R – promień krzywizny kuli ziemskiej [km],
R’– promień krzywizny toru promienia świetlnego [km],
h – wysokość.
Rzeczywista odległość obserwatora do widnokręgu (d = 3,86√h) przy standardowych warunkach atmosferycznych jest więc o około 8% większa niż odległość do widnokręgu z pominięciem efektu zjawiska refrakcji atmosferycznej (d = 3,57√h). Zasięg wzroku obserwatora stojącego nad brzegiem morza (h = 1,7 m) obliczony za pomocą wzorów geometrycznych wynosi więc ok. 4,6 km, natomiast dzięki refrakcji atmosferycznej obserwator może zobaczyć obiekty położone ok. 400 m dalej, w odległości ok. 5 km.